【クリスマス2021】ケーキの切り分けと称した資源配分問題

メリークリスマス！　この記事は 物工/計数 Advent Calendar 2021 - Adventar の第25日目（最終日）の記事です。

前提知識

　途中までは特に何の知識もなく読めます。後半は、ラグランジュの未定乗数法、および数理計画法の「相補性条件」の知識*1を前提とします。（一か所を認めれば、これを知らなくても読むことができます）

やや唐突な問題設定

　クリスマスなのであなたはケーキを焼きました。ケーキを $r$ 個に切り分け、$n$ 人の子供たちに配ります。子供 $i~(1 \leq i \leq n)~$がケーキを $x$ 個貰った時の満足度を $f_i(x)$ で表しましょう。$f_i$ は0以上の整数から実数への関数です。どんな配分をすれば、満足度の和を最大にできるでしょうか？すなわち、$\sum_{i=1}^n x_i=r,x_i \geq 0$という条件のもとで、$ \sum_i {f_i(x_i)}$を最大化するようなアルゴリズムを考えてください。

この問題を資源配分問題と呼びます。

【資源配分問題】

　$\sum_{i=1}^n x_i=r,x_i \geq 0,x_i \in \mathbb{Z}$という条件のもとで、$ \sum_i {f_i(x_i)}$を最大化せよ。

クリスマスケーキはこじつけです。

関数fの制約

　関数$f_i$に何の制約も与えないと、効率的なアルゴリズムを作るのは難しそうです。そこで、任意の$t \geq 0$に対して $f_i(t+2)-f_i(t+1) \leq f_i(t+1)-f_i(t)$ という制約を考えましょう。これは、「$t$ が大きくなるほど$f_i$の上がり幅が減る」ことを表しています。例えば、ケーキを1個ももらえないのは明らかに激烈に不満なので、$f(1)-f(0)$はとても大きいでしょう。ケーキをもらいすぎると、もらえる数が増えても嬉しさはたいして増えないでしょう。この辺りの直感を単純化したのが上記の制約です。

　実はこの制約を加えると、次のような貪欲法でこの問題を解くことができます。少し帰納的なアルゴリズムの書き方なのでご注意ください。

アルゴリズム1．

　$k$番目までのケーキを配り終えたと仮定する：各子供に、$x^*(k)_1, \cdots, x^*(k)_n$個配ったとする。$k+1$番目のケーキを誰に配るかを次のように決める：「$k+1$番目のケーキを配ったときに、嬉しさの上がり幅が最も上がる人に配る」。すなわち、$f_i(x^*(k)_i+1)-f(x^*(k)_i)$が最大になる$i$を考え、子供$i$にケーキを配る。

既視感

実はこの問題は、昔このブログで扱った*2問題を一般化したものです。それはこれです。

shib-e-ngineering.hatenablog.com

　この証明と同様に今回の貪欲法の正当性も証明できます。今回は正当性証明は本題ではないですが、一応略証を書いておきましょう。

【アルゴリズム1の正当性の略証】

　1番目のケーキを、$f_i(x(1)_i+1)-f(x(1)_i)$が最大となる$i$（これを$i*$とする）以外の子供$j$に配ったとする。「1番目に$i*$に配ることでより悪くない配り方を作れる」ことを示す。2番目以降、子供$i*$にケーキを配ることがあるのなら、ケーキを配る順番を入れ替えて、1番目に子供$i*$に配っても満足度は変わらない。2番目以降、子供$i*$にケーキを配ることがないのなら、「1番目に子供$j$ではなく子供$i*$に配る」という点のみを変えた配り方は、$f_i(t+2)-f_i(t+1) \leq f_i(t+1)-f_i(t)$ という制約ゆえ、元の変え方よりも満足度の和が高い。

　ゆえに、1番目のケーキは子供$i*$に配ったとしていい。これを帰納的に繰り返せば、アルゴリズム1で与えられる配り方が最適であることがわかる。■

　詳細は省きますが、プライオリティキューというものを使うことでこのアルゴリズムを$O(r \log n)$の計算量で実装することができます。

fの凸性と連続緩和アルゴリズム

　このままだと前の記事の使い回しも使い回しなのですが、今回やりたいのはここからです。$f$の制約$f_i(t+2)-f_i(t+1) \geq f_i(t+1)-f_i(t)$ を見直してみると、「増分が増えない」ことから、これが「上に凸」っぽい条件であることがわかります。実際、（整数でないところは線分で結んで）$f(t)$の定義域を実数全体に拡張したグラフは上に凸です。ここからは$f$を$-f$に置き換え「下に凸」っぽい関数とし、最大化問題を最小化問題に置き換えましょう。

　さらに簡単のため、$g(t)=f(t) (t \in \mathbb{Z})$をみたし、微分可能で下に凸である関数$g$が存在するとします。*3

　こうすると元の問題で$x$の範囲を整数ではなく非負実数にした連続緩和問題を考えることができます。

【連続緩和問題】

　$\sum_{i=1}^n y_i=r,y_i \geq 0,y_i \in \mathbb{R}$という条件のもとで、$ \sum_i {g_i(y_i)}$を最小化せよ。

　ラグランジュの未定乗数法と相補性条件より、実数$\lambda$が存在して任意の$i$について「$z_i=0 \implies g'_i(z_i)- \lambda \geq 0$かつ$z_i>0 \implies g'_i(z_i)- \lambda = 0$（★）」が成り立つことと$\{z_i\}$が上の問題の最適解であることは同値です。相補性条件をご存知でない場合はこの（★）を認めて先に進んでください。最適解を$z_i$で表します。

　ここで、次のように整数ベクトル$\{x_i\}$を構成しましょう。

　・$z_i$が整数のとき、$x_i=z_i$

　そうでないとき、

　・$g_i(\lfloor z_i\rfloor+1)-g_i(\lfloor z_i\rfloor) < \lambda$のとき、$x_i= \lceil z_i \rceil$

　・$g_i(\lfloor z_i\rfloor+1)-g_i(\lfloor z_i\rfloor)  \geq \lambda$のとき、$x_i= \lfloor z_i \rfloor$

　まず、★と平均値の定理より任意の$z_i$に関して$g_i(z_i+1)-g_i(z_i) \geq \lambda$です。さらにgの凸性より、$g_i(\lceil z_i\rceil+1)-g_i(\lceil z_i\rceil)  \geq \lambda$も従いますから、任意の$i$に対して$g_i(x_i+1)-g_i(x_i) \geq \lambda$が従います。さらに、$z_i \geq 1 \implies g_i(\lfloor z_i\rfloor)-g_i(\lfloor z_i\rfloor-1) \leq \lambda$も成り立ちます。これをまとめると

　「・任意の$i$に対して$g_i(x_i+1)-g_i(x_i) \geq \lambda$

　・$x_i >0$ならば$g_i(x_i)-g_i(x_i-1) \leq \lambda$」（♡）

　となりますが、実はこのとき、$\{x_i\}$は$r' := \sum_{i=1}^n x_i$とした場合の資源配分問題の（$r$に$r'$を代入したときの）最適解になっています。

　このことを示しましょう。実はそのために必要な議論はさっきの貪欲法の正当性証明とよく似ています。最大化問題を最小化問題に変えたことに注意してください。

【（♡）を満たす$\{x_i\}$が最適である証明】

　（♡）を満たす$\{x_i\}$をとり、$\sum_i y_i =\sum_i x_i$だが$\{x_i\}$とは異なる$\{y_i\}$を任意にとる。この$y_i$が$x_i$よりも「良くない」ことを示せばよい。$\{x_i\}$と$\{y_i\}$が異なるが目的関数（$\sum_i f_i(x_i)$）が一定なので、$x_i<y_i$かつ$x_j>y_j$となる$i,j$の組が存在する。ここで$\{z_i\}$を、「$z_i=y_i-1,z_j=y_j+1$」とし、他は$\{y_i\}$と同じにした列で定める。この時、$\sum_i |x_i-z_i|$は$\sum_i |x_i-y_i|$よりも小さいことに注意しよう。さらに、$y_i$から$z_i$に変えたとき目的関数は

　$g_i(z_i+1)-g_i(z_i) - ( g_i(z_i)-g_i(z_i-1) ) \leq g_i(x_i+1)-g_i(x_i) - ( g_i(x_i)-g_i(x_i-1) )$

　だけ下がる（この値が非負かはまだわからない）。この不等式には$g$の凸性と$x_i \leq z_i$かつ$x_j \geq z_j$用いた。さらに（♡）よりこの右辺は$\lambda - \lambda =0$

以上である。したがって$\{z_i\}$の方が目的関数を小さくできる。$\sum_i |x_i-z_i|<\sum_i |x_i-y_i|$であり、同じことを繰り返せば最終的に$\sum_i |x_i-z_i|=0$とでき、この時$x_i=z_i$であるから、$\sum_i f_i(x_i) \leq \sum_i f_i(y_i)$がいえる。

　いかにも貪欲法っぽく、「交換しても悪くならない」をうまく使った証明であるといえます。さて、$\sum_i x_i =r'$は$r$と等しいとは限りませんので、このままでは元の資源配分問題を解けたとは言えません。

　しかしながら、例えば$r'<r$のとき、求まった$\{x_i\}$は資源配分問題の$r'$での最適解ですから、ケーキの例で言うなら「ケーキを$r'$個まで配る途中の配り方」までは追えたことになります。アルゴリズム1の性質上、残りの$r-r'$個をアルゴリズム1と同じように配れば事がすみます。そして、$r'-r \leq \sum_i |x_i-z_i| \leq n$なので、この「残りの部分」は$O(n \log n)$で終了します。

　もしも$r>>n$であり、連続緩和問題の最適解を効率的に求められるのであれば、*4連続緩和問題を先に解く方が効率的な解法が求まるというわけです。なお、$r'>r$だった場合にもやはり$O(n \log n)$で$r$での最適解にたどり着けることを理論的に示せますが、そのことはここでは省略します。

まとめ

　いかがだったでしょうか。アドベントカレンダーの最終日に遅刻するのは忍びなさすぎるのですが、今なんと23時52分です。本当にギリギリで申し訳ありません。

　このように、離散的なアルゴリズムにおいても「凸性のようなもの」をうまく活用して、効率的なアルゴリズムを考えることができます。そして、「交換しても悪くならない」という貪欲法の正当性証明の常套手段は、この「凸性のようなもの」と極めて相性がいいことがわかっています。この辺りを一般化したのが離散凸解析のM凸関数などの概念です。

　最大化問題を最小化問題にすげ替えたせいでいつの間にかケーキの話は消滅していますし、クリスマスなのにクリスマスっぽい感じを出せなかったのが悲しいですが、物工・計数アドベントカレンダーのほかの記事もお楽しみいただければと思います。（改めて貼っておきましょう）

　物工/計数 Advent Calendar 2021 - Adventar

　今年もお疲れさまでした。

*1:応用物理学科では2年次の「最適化手法」という授業で学びます

*2:このブログを見たことがある人は0人だと思いますが

*3:このようにグラフを「滑らかな凸関数でつなげる」ことと、元の条件にはギャップがありますが、微分可能でなくても似たような理論が成り立つので、あくまで簡単のためです。

*4:たとえば$g$が二次関数である場合、（★）の条件を用いて直接的に解が求まります。

2層ニューラルネットワークの最適化理論

この記事は物工・計数 Advent Calendar 2021 の第9日目の記事です。掲載が遅れてしまい、大変申し訳ございません。

本体は以下のpdfです。

drive.google.com

この記事は 物工・計数 Advent Calendar 20211の第9 日目の記事です。掲載が遅れてしまい、大変
申し訳ございません。

初等幾何初心者による初等幾何のススメ

最近、オンラインの数学コンテストサイトであるOnlineMathContest(OMC)にハマっているのですが、始めたてのころ「幾何」がけっこう鬼門に感じました。
これは、大学入試や大学以降のカリキュラムで初等幾何をガッツリ扱う機会がそんなになく(個人差有)、解き方などにあまり馴染んでいなかったということが一因である気がします。

多分同じことを思っていらっしゃる方も多い気がするので、今回はあえて初等幾何の初心者である自分の目線で、最近ようやく学んできた初等幾何の捌き方を紹介してみたいと思います。
なお、この記事はOMCなどで出される求値形式の問題に特化しています。証明問題についてはまた別の技術があると思う(根本は同じかもしれませんが)ので、ここでは踏み込みません。

目次

1. そもそもどんな知識が必要か
2. 幾何の問題の具体的な進め方
3. 具体的な問題で見てみよう
4. まとめと全体的な勉強法

1.そもそもどんな知識が必要か

「初等幾何は見たこともない定理を知らないと解けないのではないか」という懸念をよく耳にします。個人的にはこれは間違いとまでは言わない*1までも、「そんなことはない」と思います。

特に、最近のOMCでは以下の【基本知識】(高校知識+ほんのちょっと)があれば充分に解ける問題がほとんどであると思います。

【基本知識】: 相似など小学校以前で習う知識は省いてあります
・三平方の定理
・正弦定理、余弦定理
・角の二等分線の定理
・メネラウスの定理、チェバの定理
・円周角定理
・円周角と中心角の関係
・円に内接する四角形(対角の和が180度、トレミーの定理)
・方べきの定理
・接弦定理
・三角形の五心の性質(詳しくは後述します)

こう見ると意外と少ないのではないでしょうか。中には高校の教科書の端っこにしか載っていなかったり、載っていても使ったことがあまりなくて記憶の片隅に放り出されていたり…などあるかもしれませんが、問題を1，2問解けばどういう定理だったか思い出せるものばかりだと思います。
太字にしたものは特に忘れ去られている傾向が強いと思いますがどれも重宝します。

とはいえ、流石に長年使っていないのでいざ問題を解くと「この定理を使えることに気づかなかった」みたいな事になって苦労する、ということがままあると思います。これに関しては「演習を積んで慣れる」が正解な気がするのですがそれだと記事が終わってしまうので、次の節では幾何の問題で具体的にこれらの基本知識を使ってどうやって解き進めるかを書いてみます。

2.幾何の問題の具体的な進め方

初心者として、幾何の問題に当たった時にどんなことをしているかをできるだけ具体的に書こうと思います。

①角度追跡
幾何は「こことここは同じ角度」「ここは有名角」など角度やその間の関係がわかると大きく進展することが多いです。一番有名な利点はもちろん「相似が見つかること」ですが、他にも二等辺三角形が見つかったり、円周角定理の逆で4点が同一円周上にあることがわかったり…など恩恵は計り知れません。ということで、同じ角度をみつけたらどんどん印をつけたりしています。この同じ角度を見つける時に、円周角定理や内心の性質などを意識すると役立ちます。あとは手詰まりになった時適当な角度を文字でおいてゴリゴリ書いていくと進んだりします。

②長さ追跡
相似やメネラウス・チェバの定理から長さ比を求めたり、方べきの定理やトレミーの定理などを使ったりして関係式を出したり、三平方の定理、正弦定理や余弦定理でゴリゴリ計算したり…など、辺の長さやその関係を解析するのももちろん必要です。最終的に長さを求めさせる問題は非常に多いので、結局これをやらないといけないことは多いです。辺の長さを文字で置いたりしますが、文字の置き方の筋が悪いと計算の難易度が爆発して詰むということが往々にしてあり、悲しいことになりがちです。*2

③共円・共線
「共円」を見つけるのも(わざわざ項目を独立させるぐらい)大事です。点の集合が共円であるとは、それらがすべて同一円周上に乗ることです。特に4点の共円がよく使われます。
これは①の角度追跡と表裏一体で、円周角定理の逆で見つかったり、対角の和が180度なので円に内接する四角形とわかったり…みたいな感じで見つけていきます。共円がわかると、方べきの定理やトレミーの定理などの長さに関する定理に繋がったりして非常に便利です。
点の集合が同一直線に乗る「共線」も重要です。角度追跡をちゃんとやらなかったり、図が雑だったりすると気づかないがちです。

④五心
三角形の五心(重心、垂心、内心、外心、傍心)が出てくる問題は非常に多く、またこれらの性質は忘れ去られていがちなのでこのあたりで吐き気を催す人が多い印象があります。
ですが、定義と基本的な性質をみるとそんなに複雑でもないことがわかります。具体的には、「高校数学の美しい物語」のこの記事 https://manabitimes.jp/math/628 と、以下に列挙する性質を抑えれば十二分に戦えます。(一部被ってます)

・内心／傍心
　内心は内角の二等分線の交点である。ある頂点から内接円の接点(2個)までの長さは等しい。面積と内接円の半径との関係S=(a+b+c)rをたまに使う
　傍心は外角の二等分線の交点で、ある頂点からひとつの傍接円の接点(2個)までの長さは等しい。

・外心
　垂直二等分線の交点である。二等辺三角形が3個できる

・重心
　頂点と対辺の中点を結ぶ線の交点である。いわゆる「2:1の性質」がある

・垂心
　共円となる4点が3つできる。相似な直角三角形がたくさんできる

・オイラー線
　重心、外心、垂心は共線である

もちろんこれで性質全部では当然なく(五心は奥が深い)、ここにない五心の面白い性質が問題で出てくることもあるのですが、それはその都度学んでいけばよいと思います。

⑤補助線
補助線をどこかで引かないと中々進展しない問題も多いです。ぶっちゃけ天才補助線を引かないと解けない問題もありますが、補助線の引き方にも一定のコツがあるようです。やっぱり「知ってる構図に帰着させる」気持ちで引いていくのが良いと思います。(一番簡単な例だと小学校の問題で相似を作るために平行線を引いたりします。)あと定石というか頻出の補助線もあって、例えば1:2の角度があったら2の方の角度を2等分したり、倒れている長方形があったら真っ直ぐ線を引いたり、円の中心から接線との接点に線を引いたり…と、この辺は本当に演習を積んで触れて慣れる感じだと思います。
これはあるあるだと思うのですが間違った補助線は結構害になることがあって、線が増えるので未知数が増えたりして手に負えなくなります。なので補助線を引くときは色を分けたりしていつでも消せるようにしています。

⑥三角関数・座標・複素平面
そもそも初等幾何で解かなければならないという縛りはどこにもないので、三角関数でゴリ押せそうとか座標が入りそうとかわかったら時間次第で躊躇なく入れるのも良いと思います。でも初等で考えたいという意地もめっちゃわかります。
複素数平面を入れられたり、複素数平面に関する知識(反転など)を持っておくと有利になることもたまにあります。

3.具体的な問題で見てみよう

①自作問題
OMCっぽい自作問題をつくったので、ここまでに紹介したノリで実際に解いてみます。(よければ考えてみてください)

まず図を書きます。ちなみに人間は3点を通る円を書くのがクソ下手らしいので円を先に書いた方が綺麗になるらしいです。
今回CO=OJなので、4点A,C,D,Jが共円であることがわかります。しかもCJは直径なのでAが直角であることもわかります。
共円や有名角が出たので、一気に①の角度追跡をやったら嬉しそうです。ADは二等分線なので45度が出てきて、円周角と中心角の関係からDOC=90°も出そうです。これは便利そうなのでDOに補助線を引いておきます。さらに、円周角定理から角DCOが45度であるとわかります。直角二等辺三角形が出てきましたね。(実はこれは上で述べた外心の性質「二等辺三角形が出てくる」からもわかります)

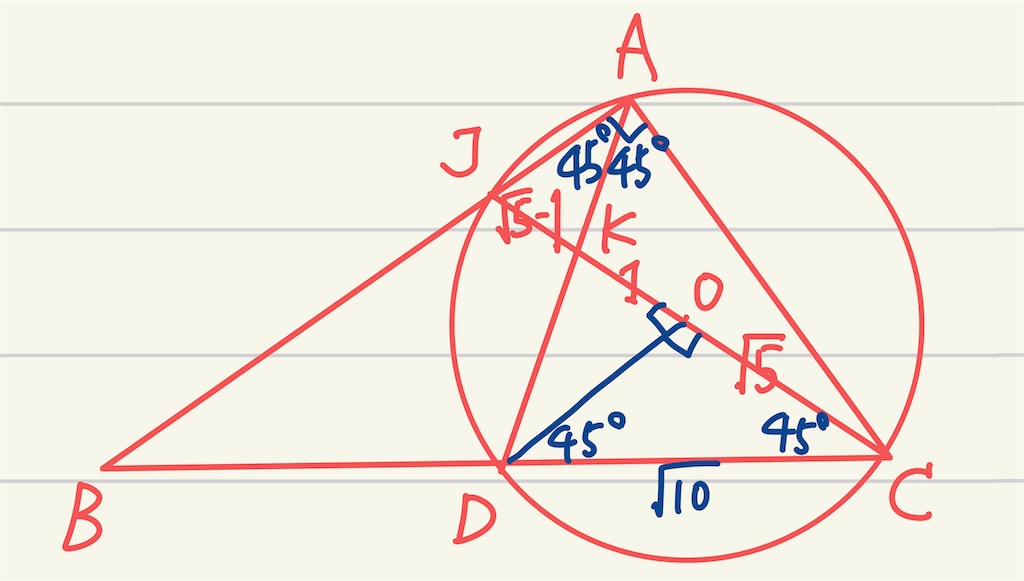
ここまでの図です。さて、ここからは適当な辺を文字で置いて、三平方の定理や角の二等分線の定理などで③の長さ追跡を頑張ると解けるのですが、もう少し①の角度追跡を粘ってみます。というのも直角三角形が色々出てきたので、相似がまだ見つかるかもしれないからです。角ODKをxとおいて角度を追跡すると

このようになって、ABCとODKの相似がわかりました！相似がわかる瞬間は気持ちいいですね(相似比が結局わからずボツになることも多いですが)。今回は辺の比が1:√5とわかっているので最後に角の二等分線の性質を使ってBD=√50=5√2がわかり、答えは5√2+√10となります。

まとめと全体的な勉強法

というわけで具体的な話に終始してしまいましたが、そんなに知識を詰め込むという感じでなくとも充分に幾何は楽しめると思います。そして今回紹介したような解き方を実践するためにはやはりOMCの過去問やJMOの予選の過去問などを解きまくるのが良いと思います。個人的にはまず粘って解いて、解答がもっと綺麗だったらそれにも目を通すみたいにやっています。たまに死ぬほど難しい問題が出てきて絶望しますがそれも含めて楽しいです。幾何得意になりましょう！！！(僕がなりたいまず)

*1:確かに例えばOMCでは、根心や等角共役点など高校で出てこないかなり深めの概念を使わないとほぼ解けない問題も「たまに」あります

*2:でも大学入試も「計算が楽になる文字の置き方ゲー」みたいな問題がたくさんあった気がするので、むしろ慣れているかも

最小全域木問題の「凸性」②

前回の記事　の続きです。

前回は、最小全域木を求めるアルゴリズムとその「凸っぽさ」を定義し、離散版の凸関数を定義する必要性を述べた。ここからはいよいよその定義に入る。

3.「離散版」凸関数の定義（M凸関数）

まず、ユークリッド空間で定義された関数$f: \mathbb{R}^N \to \mathbb{R}$の定義は以下のようであった。

定義（凸関数）：$f: \mathbb{R}^N \to \mathbb{R}$が凸関数であるとは、任意の$x,y \in  \mathbb{R}^N$および$0 \leq t \leq 1$に対して$f(tx+(1-t)y) \leq tf(x)+(1-t)f(y)$が成り立つことである。

上記の定義の$t$に$\alpha (0 \leq \alpha \leq 1)$と$1- \alpha$を代入して辺々足し合わせると、凸関数では$f(x+\alpha(y-x))+f(y+\alpha(x-y)) \leq f(x)+f(y)$が成り立つことがわかる。つまり、任意の$x,y$を取ったとき、両端$x,y$から$\alpha$だけ「歩み寄った」点$x+\alpha(y-x),y+\alpha(x-y)$での$f$の値の和は、両端での$f$の値の和以下になる。

ところで逆に、$f(x+\alpha(y-x))+f(y+\alpha(x-y)) \leq f(x)+f(y)$が成り立つとき、$f$は凸関数と言えるだろうか。実は$f$が連続であれば凸関数と言える（解析をゴリゴリやると出来るが、本筋から逸れるので省略する）。開区間で定義された凸関数は連続なので、$f: \mathbb{R}^N \to \mathbb{R}$であれば$f(x+\alpha(y-x))+f(y+\alpha(x-y)) \leq f(x)+f(y)$は$f$の凸性と同値になる。

この$f(x+\alpha(y-x))+f(y+\alpha(x-y)) \leq f(x)+f(y)$の方を離散っぽく言い換えることにする。$f$の定義域を$\mathbb{R}^N$ではなく$\mathbb{Z}^N$にすれば離散的になりそうだ。しかし、$x,y \in \mathbb{Z}^N$に対して、たとえば$x+\alpha(y-x)\in \mathbb{Z}^N$とは限らないので工夫が必要である。この辺りに注意して書き換えたのが以下のM凸関数である。

定義（M凸関数）：関数$f:S \subset \mathbb{Z}^N \to \mathbb{R}$がM凸関数であるとは、任意の$x,y \in \mathbb{S}^N$をとったとき、$x_i-y_i >0$をみたす任意の$i$に対して$x_j-y_j <0$をみたす$j$が存在して、

　　$x+e_i-e_j,y-e_i+e_j \in S \land f(x+e_i-e_j)+f(y-e_i+e_j) \leq f(x)+f(y)$

が成り立つことをいう。ただし、$e_i$は第$i$成分のみ$1$で他は$0$である単位ベクトルである。

凸関数を定義するときに凸集合も定義したのと同様、M凸集合も定義しておく。

定義（M凸集合）：関数$f:S \subset \mathbb{Z}^N \to \mathbb{R}$がM凸集合であるとは、任意の$x,y \in \mathbb{S}^N$をとったとき、$x_i-y_i >0$をみたす任意の$i$に対して$x_j-y_j <0$をみたす$j$が存在して、

　　$x+e_i-e_j,y-e_i+e_j \in S$

が成り立つことをいう。

定義から明らかに、M凸関数の定義域はM凸集合である。

この定義は一見、随分と本来の凸関数（や凸集合）の定義を弱めたように見える。ある方向$i$に対して、「$i,j$方向に歩み寄って小さくなる方向」$j$が一方向でも存在すればよいことになる。また、$x_i-y_i$と$x_j-y_j $の符号が違う必要があるのがなぜかもまだよくわからない。となると、凸関数のうれしい性質と似たものが復元できるのだろうかと不安になる。

一旦その不安は胸にしまい、以下ではまず全域木の重みがM凸関数になっていることを確認し、そのあとでM凸関数における最適化の様々な性質を見ていく。

4.全域木のM凸性

勘がよい方はもうお気づきのことと思うが、全域木の集合はM凸集合になり、全域木の重み（辺の重みの総和）はM凸関数になる。これは次のようにすればよい：

命題2：グラフ$G=(V,E)$とし、以下では辺の部分集合からなる集合族$2^E$を$\{0,1\}^{|E|} \in \mathbb{Z}^{|E|}$と同一視する：$S \in \{0,1\}^{|E|}$を$E$の部分集合と同一視し、$S_i=1$ならば辺$i$が$S$に含まれていることを表すものとする。

この時以下が成り立つ。

1. $\mathcal{S} :=\{S \in 2^E \mid Sは全域木 \}$とすると、$\mathcal{S}$は凸集合である。
2. $w:\mathcal{S} \to \mathbb{R}$を$w(S)=（Sの辺の重みの総和）$と定めると、$w$は$S$上のM凸関数である。

命題2の証明は、定理1の証明を思い出すと出来る。定理1では、異なる全域木$S,T$を取ったときに、$e \in S \setminus T$に対して$f \in T \setminus S$をとり、$T \cup e \setminus f$が全域木となることを用いて証明をした。これはそのまま命題2の1.の結果である。

証明　

1.) $T,S \in \mathcal{S}$を取る。$S$と$T$の$\{0,1\}^{|E|}$での表現を考えると、$S_i-T_i>0$となる$i$が存在することは、$S \setminus T$が空でないことと同値である。最小全域木の辺数は常に一定なので、この時$T \setminus S$も空でない。ここで定理1の証明と全く同様にして、$T \setminus S$から辺$f$を選び$T \cup e \setminus f$を全域木にできる。$S \cup f \setminus e$が全域木となることも明らかであるから、この$f$が（M凸関数の定義で存在が要請される）$j$に対応する。■

2.) 1.)のように$e,f$を選んだ時、明らかに$w(T \cup e \setminus f)+w(S \cup f \setminus f)=w(T)+w(S)$なので、$w$はM凸関数の定義における不等号（の等号成立条件）をみたす。■

というわけで、最小全域木問題をM凸関数の最小化問題に焼き直すことができた。ここまでくれば、あとはM凸関数の一般的な性質、特に「極小解⇒最小解」を調べればよい。実はもう道具はそろっていて、やはり定理1の証明を一般的に焼き直せばよい。以下ではそれを見ていく。

5.M凸関数の性質

「極小点」は次のように定義するのが自然であろう。

定義（極小点）　$S \in \mathbb{Z}$、$f:S \to \mathbb{R}$とする。$x$が$S$における$f$の極小点であるとは、$x+e_i-e_j \in S$をみたす任意の$i,j$に対して、$f(x+e_i-e_j) \geq f(x)$をみたすことをいう。

次の定理は重要である。

定理3　M凸関数において、極小点は最小点である。

参考文献を見たら証明が全カットされていて悲しい気分になった。自分で構成した。

証明　$S$をM凸集合、$f$をM凸関数とする。$x$を$S$における$f$の極小点とし、$y \in S$が$f(x)>f(y)$をみたすと仮定して矛盾を導く。

ここでは$x$と$y$の$L^{\infty}$距離（各成分の差の絶対値の総和$\sum {|x_i-y_i|}$）$d(x,y)$に関する帰納法により、任意の$d(x,y)$で矛盾が生じることをを示す。$d(x,y)=0$で矛盾が生じるのは自明である。$d(x,y) \leq n$で矛盾が生じるとする。$d(x,y)=n+1$として矛盾を導く。 

いま$x \neq y$である。$x_i-y_i >0$となる$i$が存在するとして一般性を失わない（必要であれば$x$と$y$を入れ替えればよい）。この時M凸集合およびM凸関数の定義から

$x_j-y_j <0$をみたす$j$が存在して、

　　$x+e_i-e_j,y-e_i+e_j \in S \land f(x+e_i-e_j)+f(y-e_i+e_j) \leq f(x)+f(y)$

が成り立つ。ここで$x$の極小性より、$f(x+e_i-e_j) \geq f(x)$なので、$f(y-e_i+e_j) \leq f(y)$でなければならない。このとき仮定$f(x)>f(y)$より$f(x)>f(y-e_i+e_j)$である。しかし$L^{\infty}$距離に注目すると、$d(x,y)<d(x,y-e_i+e_j)$なので、帰納法の仮定から矛盾が生じる。ゆえに任意の$d(x,y) \leq n$で矛盾が生じるので、結局任意の$y \in S$に対して$f(x) \leq f(y)$であり$x$が最小点となる。■

この証明の「凸関数っぽい」見方を併記しておく。第3項の最初で述べた通り、（連続版でも）凸関数では「歩み寄ると和が小さくなる」という性質がある。凸関数の極小点$x$と、そうでない点$y$を取ったとき、$x$の近傍からはみ出さない程度の幅で$x,y$同時に歩み寄ると、和は小さくなるが、$x$は極小点なので$y$から歩み寄った点$y'$での関数の値$f(y')$は$f(y)$以下である。$y$を$y'$に入れ替えると$x,y$は近づいていて、同じことを（$x$と$y$の距離）/（$x$の近傍の大きさ）回ぐらい実行すれば$x=y$となり、ゆえに$f(x) \leq f(y)$でなければいけなくなる。

このように見ると、やや弱いように見えたM凸関数の定義は、「極小⇒最小」という意味での凸関数の性質をとらえるには充分であることがわかる。

さらに以上から、定理3の系として定理1が得られる。これにより、最小全域木問題のM凸関数最小化問題としての定式化が無事できた。

以上により、クラスカル法やカラバ法の正当性証明において重要な役割を果たした定理1を、M凸関数の観点から理解することができた。一般化することのメリットは非常に大きく、全域木問題に限らず構造にM凸性を有する問題に対して似たようなアルゴリズムを利用することができる可能性もわかった。

一方で、定理1のみではクラスカル法やカラバ法を導出するにはややギャップがある。定理1によりいわば「極小全域木」をとってくれば良いのだが、クラスカル法やカラバ法では「極小全域木を作る上で『いらない辺』を巧妙に除去できている」ことが本質的に重要であった。このような性質もM凸関数の観点から書き直せないだろうか？

これは、実はM凸関数のカット定理とよばれる定理で記述することができる。しかし、長くなるうえに特にクラスカル法に関してはM♮凸という概念も導入しないといけないので今回は一旦ここで切ろうと思う。

最小全域木問題の「凸性」①

☆この記事は、室田一雄・塩浦昭義『離散凸解析と最適化アルゴリズム』の1章及び8～13章をを参考にしていますが、証明の流れや定理の置き方などがかなり大幅に変わっています。誤りがあったらご報告いただけますと幸いです。

はじめに

重み付きグラフの全域木のうち、辺の重みの合計が最小になるものを求める問題を最小全域木問題と呼ぶ。

突然だが、「最小全域木問題は『離散版の凸関数の最大化問題』に帰着する」と言われてピンとくるだろうか。少なくとも僕はこの文章だけ見たら全然ピンと来ない。でも学んでいくうちに、確かに最小全域木の「凸っぽさ」が現れてきて、離散的な凸関数を定義することでこの文章の厳密な意味もわかる。そこで本稿ではまず、「最小全域木の凸っぽさ」をなんとなくつかめるようにして、アルゴリズムを紹介し、そこから離散的な凸関数を厳密に定義して、アルゴリズムを一般的な観点から再導出するという流れで話を進める。

この記事は3回に分け、今回は最小全域木の「凸っぽさ」の紹介とアルゴリズムの紹介・正当性の証明をおこなう。次回離散版の凸関数を定義し、そのうえでの最適化アルゴリズムを紹介して今回のアルゴリズムとの関連を述べる。3回目でより発展的な話題につなげる。

本稿の前提知識はグラフの基本的な用語および凸関数の定義・基本的な性質のみである。

1.最小全域木問題の「凸っぽさ」

辺に重み$w( \cdot )$がつけられた無向グラフ$G=(V,E)$の最小全域木とは、全域木（$G$の全頂点を要素に持つ木）であって、辺の重みの合計が最小になるものをいう。*1

$G$の最小とは限らない全域木$T$をひとつ取る。$T$よりも重みの小さい全域木を作りたかったら、どうすればよいだろうか？

$T$に含まれない辺$e$をひとつとる。$T$に$e$を付け加えると閉路（サイクル）が一つできる。この閉路を$C(T,e)$と書く。$C(T,e)$に含まれる辺$f$で$e$と異なるもの（これは$T$の要素である）を一つ選び$T \cup e$から除くと、$T \cup e \setminus f$は$T$とは異なる全域木になる。ここで、$w(e) < w(f)$が成り立つなら、新しくできた全域木$T \cup e \setminus f$は重みが$T$より真に小さい。*2

逆にいえば、$T$が最小全域木ならばこのようなことはできないはずだ。つまり、$T$が最小全域木ならば、「任意の$e \not\in T$と$f \in C(T,e)$に対して$w(e) \geq w(f)$」…（★）である。

 （★）の条件は、「極小」に近い概念に見えないだろうか。関数の極小点と言われれば、近傍が存在して近傍内で最小になるような点であるが、上記のように$T$から辺$e$と$f$を入れ替えて到達できる全域木を「近傍」のように見るとすると、あたかも（★）は$T$の極小性を言っているように見える。そうすると、$T$が最小全域木ならば（★）が成り立つことも「最小⇒極小」というごく当たり前の性質に見えてくる。

ここで非自明なのは、今述べたことの逆が成り立つことである。すなわち、$T$が（★）をみたすならば、実は$T$は最小全域木になる。これを証明しよう。

定理1　任意の$e \not\in T$と$f \in C(T,e)$に対して$w(e) \geq w(f)$ が成り立つならば、$T$は最小全域木となる。

証明　もしも$T$より重みの真に小さい全域木$S$が存在したとする。$S,T$の辺の要素数は$ |V|-1$で等しいことに注意すると、$S \setminus T = \emptyset$だと$T=S$となり矛盾するので、$S \setminus T \neq \emptyset$である。

$S \setminus T$から辺$e$を選ぶ。$C(T,e)$の要素のうち$e$と異なるもので、さらに$S$に含まれないものをひとつとり$f$とする。もしそのような辺が存在しないと、$C(T,e)$の要素はすべて$S$の要素となり、$S$に閉路が存在することになり矛盾する。とり方より$f \in T \setminus S$である。ここで$T' =T\cup {e} \setminus {f}$とすると$T'$は全域木で、$T'$と$S$の共通部分の大きさは$T$と$S$のそれよりも1だけ大きくなっている。また定理の仮定より、$T'$の重みは$T$の重み以上である。このように$T$を更新することを繰り返せば最終的に$S$と等しくなり、したがって$S$の重みは$T$の重み以上である。これは最初の仮定に矛盾するので、$T$は最小全域木である。■

証明は意外にも単純であるが、ここで重要なのはこの定理が（気持ちとして）「極小⇒最小」を表していることである。こう見ると、早くも「凸っぽさ」がお分かりいただけたと思う。よく知られているように凸関数では、極小値がそのまま最小値になっている。

ただしもちろん「へえじゃあ最小全域木問題は凸関数なのね」と早合点することはできない。この場合の近傍は普通の実数での近傍と同じ意味では当然ない。また、ここでいう凸関数の定義域は全域木の全体で、各全域木に評価値が定義されていると思うと、定義域は実数のような連続的なものではなく、離散的なものである。この辺りを厳密に書くには凸関数の離散版のような定義が必要そうだ。そこでこの問題はいったん棚に上げることにして、最小全域木を求めるアルゴリズムを2つ紹介する。

2.最小全域木を求めるアルゴリズム

2-1.クラスカル法

クラスカル法は、貪欲法（その場で最良のものを選択する）によって最小全域木を求めるアルゴリズムである。具体的には、次のように求める。

アルゴリズム1（クラスカル法）

　グラフを$G=(V,E)$とし、辺集合$T$をはじめ空集合とする。次の順番で$T$に辺を加えていく。まず、$T= \emptyset$に、$E$の辺で重みが最小の辺を加える。以降は、まだ加えていない$E$の辺で、加えても$T$に閉路ができないもののうち重みが最小の辺を加える。

このようにクラスカル法は「加えられる辺のうち一番良いものを加えていく」という貪欲的なもので、実装も楽で非常に有名なアルゴリズムである。競技プログラミングなどをやっている人は親の顔より実装していそうだ。

これが全域木を出力して停止することは少し考えれば明らかなので省略する。一方、「最小」全域木を出力することは全く自明ではない。これの証明はよい演習問題のようでどの本にも載っている。*3ここでは、定理1を用いることでシンプルに証明する。

証明（クラスカル法の正当性）

全域木を出力することの証明は省略する。クラスカル法を次のように等価に言い換えておくと見通しが良い。

「辺集合$T$をはじめ空集合とする。$E$を辺の重みが小さい順に並べ替え$ \{e_1, \cdots,e_m \}$とする。$k = 1,2, \cdots, m $の順で$T$に$e_k$を加えていく。但し$T$に$e_k$を加えたとき閉路ができてしまう場合は加えない。」

紛らわしいので今後$T$は最終的にできた全域木を表すものとする。ここで、クラスカル法において加えられなかった辺全体の集合が$E \setminus T$であることに注意する。加えられなかった辺$e \in E \setminus T$は、「加えると閉路ができてしまう辺」であり、その「閉路」とは$C(T,e)$に他ならない。$C(T,e)$の$e$以外の要素は$e$以前に加えられた辺なので重みは$e$のそれ以下である。ゆえに定理1より、$T$は最小全域木である。■

このように定理1を用いてうまく証明できることを見ると、この貪欲法は実は「加えなくていい辺を見事にスルー」できていることがわかる。

2-2.カラバ法

最小全域木を求めるもうひとつのアルゴリズムであるカラバ法を紹介する。クラスカル法が空集合から徐々に木を構成していくのに対し、カラバ法はまず全域木を適当に作り、それを「改善」していく。

アルゴリズム2（カラバ法）

　グラフを$G=(V,E)$の頂点数を$n$,辺数を$ m $とする。$G$の最小全域木$T_0$をひとつとる。$F=E \setminus T_0 =\{f_1,\cdots,f_{m-n+1} \}$として、$t=1,\cdots,m-n+1$において次のステップ$t$を実行する：

　ステップ$t$：$T_{t-1}$に$f_t$を加えると閉路$C_t=C(T_{t-1},f_t)$がひとつできる。$C_t$を構成する辺のうち重み最大のものを$e_t$とする（複数ある場合は一つ適当に選ぶ）。この時、$T_{t-1}$に$f_t$を加えたあと$e_t$を除去したものはまた全域木であるからこれを$T_t$とする。

　最終的にできた$T_{m-n+1}$が出力である。

このアルゴリズムは計算量がヤバそうだが、何も考えずに木を良い方向に更新するのではなく、閉路で一番重みの大きいものを除去するという工夫をするだけでステップ数が$m-n+1$になっている。しかしなぜこれで最小全域木が出力されるかはやはり自明ではない。以下ではまた定理1を用いて正当性を証明する。

証明（カラバ法の正当性）

$T:=T_{m-n+1}$とする。一度除去された辺は二度と追加されないので、$\{e_1, \cdots,e_{m-n+1}\}=E \setminus T$である。クラスカル法のときと同様、「$C(T,e_t)$の任意の要素の重みが$e_t$の重み以下である」…（☆）ことを示せばよい。$C(T_{t},e_t)=C(T_{t-1},f_t)$なので、$C(T_{t},e_t)$の任意の要素の重みが$e_t$の重み以下であることは自明であるが、$C(T,e_t)$と$C(T_{t},e_t)$は異なるので少し注意しなければならない。

（☆）を帰納法で示す。$u \geq t$とする。$e_t$が$C(T_u,e_t)$で最大の重みをもつとして、$C(T_{u+1},e_t)$でも最大の重みをもつことを示す。

$C(T_u,e_t)=C(T_{u+1},e_t)$のときは良い。$C(T_u,e_t) \neq C(T_{u+1},e_t)$となるのは、ステップ$u+1$で$C(T_u,e_t)$の構成要素$e_{u+1}$が除去されるときである。この時、$C(T_{u+1},e_t)$はふたつの閉路の「合成」となる：$C(T_{u+1},e_t)=C(T_u,e_t) \cup C(T_u,f_{u+1}) \setminus e_{u+1} $である。ここで、$w(e_{u+1}) \leq w(e_t)$かつ$e_{u+1}$は$C(T_u,f_{u+1})$で重み最大の辺であることに注意すれば、$e_t$は$C(T_{u+1},e_t)$でも重み最大の辺となる。

$u=t$での成立は自明であるから、帰納法より$e_t$は$C(T,e_t)$の要素の中で重みが最大である。ゆえに定理1から、$T$が最小全域木であることが従う。■

カラバ法はクラスカル法と全然違うアルゴリズムに見えるが、「要らない辺を的確に除去している」という点ではクラスカル法とある意味似ていることがわかる。ただし、計算量はクラスカル法の方がよさそうである。*4

今回の議論を軽くまとめる。最小全域木問題はある種の「凸っぽさ（極小⇒最小）」を持っていることを示した（定理1）。次に定理1を用いて、2種類のアルゴリズムの正当性を示した。

繰り返しになるが、このように考えたときの「凸関数」の定義域は離散的である。すると今度は、「離散的な凸関数」を厳密に定義して以上の議論を一般化し、今出た2種類のアルゴリズムを導出してみたくなる。以下ではそれをやっていく。

*1:最小全域木は改めて重要性を述べるまでもないぐらい有名な概念だが、たとえば辺の重みを通信にかかるコストだと思えば、例えばすべての住宅（全頂点）を結ぶ通信ネットワークの効率最適化に応用できる。

*2:単一辺の集合$\{x\}$を$x$と略記する。

*3:しかし、私は怠惰なことに一度も証明を読んだことがなかった。

*4:カラバ法で重いのは、閉路の中で最大の重みの辺を求めるところであろうが、ここを工夫したら計算量を落とせそうだ。でも、そういう工夫をしていると知らないうちにクラスカル法に行きついていそうだ。

OMCG(幾何コンテスト) A~F

最近OMC ( onlinemathcontest.com ) にハマっている。超雑に言うと数学版AtCoderみたいな感じの数学コンテストサイトである。
OMCをやる上で一番の課題は幾何である。ベクトルや三角関数はまだしも、初等幾何は大学に入って以降はおろか大学入試ですらまともに触れた覚えがない。なので幾何力をつけないと必ず爆死する。

OMCの過去のコンテストを漁っているとOMCGという幾何だけが出るコンテストがあった(1回しか開催されていないが)。

コンテストのリンク→ https://onlinemathcontest.com/contests/omcg001

なのでとりあえずAからFまで解いてみた。だいたい4時間半で解けたのでコンテストに参加していたら25位ぐらいだと思う。

ちなみに問題ごとの正答者数はこんな感じで、G以降は地獄っぽい。

(以下、OMCGのネタバレを含みます)

各問題の解答(実況風)

以降、各問の解答をまとめる。幾何の解答をかっちり書くのは面倒だし、折角のブログなので、「実況風」にざっくりした解答(方針に近い)を書いてみる。もちろん最後の結論まで書く。

A問題

ぶっちゃけ一番苦戦した。なんで200点なのかよくわからない。

図。まず直角二等辺三角形BDEの1辺の長さを求めたくなる。これは、BからACに垂線Hを引き、三平方の定理を用いることで15√17/13という(顔を顰めたくなるような)長さがすぐ出る。
しかし、ここからがなかなか思いつかない。
BCFとDEFの面積比を求めればいいのだが、このふたつの三角形は三角形BDFと隣り合っているで、DFやBFの長さが求まれば、辺の長さの比を用いて解決しそうだ。
しかしそれがわからない。
焦って順位表を見ると10分以内に解いている人が誰もいなかった。やばいと判断して後回しにすることに

(200分後)

すこし進展。先程おろした垂線BHを延長し、DEとの交点をIとする。HIDとHDBが相似であることに注目すると、DI:IE=1:3が出る。しかし、相変わらず(目標である)DFやBFの長さはわからない。うーん

あ、僕は大事なことを忘れていた。メネラウスの定理だ。

BE:FE=1:k,FH:HD=l:1とする。メネラウスの定理が使えて、l=3kがわかる。
lをkで表せたので、kを求めれば良い。BFの長さをkを用いて2通りに表す。一つ目はBIとIFの三平方の定理、二つ目はBEとの長さの比である。これでk=4/5と求まる。あとはDFとBFの長さを求めておしまい。

三角関数や座標を入れるともっと簡単に解けるのかもしれないが、初等的な方法のみで解いていきたかったのでこうなった。難しかった。
と思って解説を見たら思いっきり座標入れてた。草

B問題

大学入試っぽい。軌跡の周囲はどう考えても円なので、その中心がどこかを予想して、予想が正しいことを証明すればよさそうだ。

弧ABの中点をMとして、MAを半径とする円になりそうである。これをどう証明するかだが、三角関数でパラメトライズしても良いが、円周角定理を用いるともっと楽にできそうだ。

超雑な答案は上の通り。円周角定理の逆が使えるのは、1回目の円周角定理でPQBが正三角形であることがわかり、角PQB(=角AQB)が常に60度になることがわかるからである。そういうことは答案に書けや

これはそんなに難しくなかった。

C問題

図。ちょっととっつきどころがない気がするが、角B,Cの二等分線を入れてみたくなる。すでにある角Aの二等分線と含めた3つの二等分線は、内心で一点に交わる。

この補助線を引けば相似な三角形がふたつ出てきて上図のようにすぐ解決する。字汚くてごめん
終わってみるとシンプル　ちなみに本当は結構グダリました

D問題

このあたりから難易度が上がってくる。今思うと上の図は嘘で、CDOが垂直だからCDと円は接するはずだ。それを完全に忘れていたがそれでもこの問題は解ける。

すぐにわかるのは、OからABに垂線OHを下ろすと3:4:5の三角形が現れることである。
次に、CODが直角なので3点DOHが共線(一直線上にある)であることがわかる。また、DECが二等辺三角形であることが次のようにして示せる。

角DAOを丸、角OABをバツとする。から、角DCEは「丸+バツ」であるとわかる。また角DCEも円周角定理より「丸+バツ」である。よってDECは二等辺三角形である。

ここまでくれば面積を使って解決する。
解説してみると思ったより簡単だった。でも解いてる時は結構難しかった。

E問題

いかにも座標を入れたくなる設定なので、座標に近い発想をすれば良さそうである。そこで正方形EFGHを真っ直ぐな正方形で囲い、図のように長さx,yを考えてあげる。

すると相似比からDK=BJ=3xが従う。

あとは芋づる式に書き込めて、三平方の定理をAEとBEについて用いれば非常に綺麗に解決する。なお、求める面積は三平方の定理よりx^2+y^2に等しいことを使うと計算が楽になる。

これは思いつかないと相当難しいと思う。自分は似たような解法の問題をどこかで【数学実況#1】数学オリンピック 予選 - YouTube見たことがあるので解けた。座標を入れても変数をうまく設定すれば実質的に同じ発想ができると思う。

F問題

ぶっちゃけAからFの中で一番簡単だった。とくにコメントがないので解答をいきなり貼る。

CEとDAを延長した交点をP、CEとDBの交点をQとすると、PD:DC=DQ:QBが相似比よりいえる。一方、角の二等分線の性質からDQ:QB=DE:EBでもある。この二つを連立することにより長さが求まる。一瞬グロテスクな二次方程式が出現するが、OMCは電卓の使用を推奨しているので慌てず解の公式を用いると判別式が360000となり、ちゃんと有理数解になる。

ちなみに、Pを取ることが思いつかなくても余弦定理を用いることもできる。A問題と交換した方がいいのではないか？

所感

幾何の問題は解いている時は地獄なのに、解き終わって振り返ると「なんだこんなもんか」となりがちで少し悲しい。しかし解けた瞬間はめっちゃ嬉しい。今度は場合の数編もやりたい。

貪欲法を丁寧に証明してみた CODE THANKS FESTIVAL 2017(Parallel) C問題編

貪欲法の証明は難しいことが多い。（学科のレポート課題で死んだトラウマ）

こういうときは問題を解いた後丁寧に証明を書くことで、理解が深まるらしい。そこで、AtCoderで貪欲法の問題を解いたらたまに証明をなるべく丁寧に書いて載せてみようと思う。

今回の問題

atcoder.jp

概要：機械が$N$台あり、$i$番目の機械は初め$a_i$秒でプレゼントを1個作れる。ただし1個作るごとに、（1個作るのに必要な時間が）$b_i$秒ずつ増えてしまう。違う機械を同時に使うことはできない。

どの機械をいつ使うかをうまく選んで、$K$個のプレゼントをできるだけ早く作りたい。$K$個のプレゼントを作るためにかかる最小の時間は何秒か？

答えの方針

直感的には、プレゼントを1個作るごとに「いま一番速い機械」を選べばよさそうである。つまり、プレゼントを$t$個作った後の機械$i$の速度（プレゼント1個を作るのに必要な秒数）を$a_i^t$として、$a_i^t$が最小となる$i$を$i+1$回目の機械に選べばよい。

証明

$t ~(1 \leq t \leq K)~$回目に選ばれる機械の番号を並べた列を$x_1 \cdots x_K$とする。さらに、$a_i(=a_i^0)$が最小である$i$を$i^*$とする。

「問題の最適解（$K$個作るのにかかる時間が最小となるような列）で、$x_1=i^*$であるようなものが存在する（★）」ことを示す。

もしも（★）が示せれば、2回目に選ぶ機械についても、$a_i^1$が最小になるものを選ぶような最適解が存在することを同様に示せる。これを$K$回繰り返せば証明が終わる。

（★）の証明：

もしも$x_1=i^*$となる最適解が存在しないと仮定する。適当な最適解$x_1 \cdots x_K$を一つ取る。ここで、$x_1 \cdots x_K$を適当に並び替えても、最終的にかかる時間が変わらないことに注目すれば、（各機械が選ばれた回数のみによって最終的な時間が決定することは容易にわかる）$x_t = i^*$となる$t$は存在しないことがわかる。

そこで、この最適解$x_1 \cdots x_K$の$x_1 \neq i^*$を$i^*$に置き換える。すると、もちろん1個目のプレゼントを作るのにかかる時間は減少し、2個目以降のプレゼントを作るのにかかる時間も、$x_2$以降に$i^*$は現れない（つまり劣化の影響を受けない）ので増加することはない。（むしろ、$i^*$に置き換える前の$x_1$が1回目で劣化しなくなるので、速くなる可能性がある）。したがって、$x_1 \neq i^*$を$i^*$に置き換えた列$i^* \cdots x_K$もまた最適解である。これは最初の仮定に矛盾するので、背理法により（★）が示された。■

感想

貪欲法の証明の定石は「貪欲でないところを貪欲なものに入れ替えても悪化しない」ことを示すことである（らしい）。ただし毎度（個人的に）発生する問題は、入れ替えによって後の方に影響が出ることをどう処理するかが難しいところである。

たとえば今回の例では、$x_1 \neq i^*$を$i^*$に置き換えた場合に、$x_2$以降に$i^*$が含まれていると、それが劣化の影響を受けて遅くなるため、一概に「悪化しない」とは言えない。この可能性をあらかじめ封じるために、入れ替えで不変であることに着目した。

こういうのを頭の中でぱっと思いついて実装できる人はすごいと思う。

（おまけ）実装

Submission #24057249 - CODE THANKS FESTIVAL 2017(Parallel)

プライオリティキューを用いた。まずプライオリティキューに組$(a_i,b_i)$を全部入れて初期化し、$t~(1\leq t \leq K)$回目の操作では、$a_i$が最小となる組を取り出し、$a_i$に$b_i$を加算して挿入する。初期化が$O(N)$,取り出しや挿入に$O(logN)$かかるので、結局$O(N)+O(KlogN)$かかる。これは、制約のもとで間に合う。